面试官：说说你对集合的理解？常见的操作有哪些？

一、是什么

集合（Set），指具有某种特定性质的事物的总体，里面的每一项内容称作元素

在数学中，我们经常会遇到集合的概念：

  • 有限集合：例如一个班集所有的同学构成的集合
  • 无限集合：例如全体自然数集合

在计算机中集合道理也基本一致，具有三大特性：

  • 确定性：于一个给定的集合，集合中的元素是确定的。即一个元素，或者属于该集合，或者不属于该集合，两者必居其一

  • 无序性：在一个集合中，不考虑元素之间的顺序，只要元素完全相同，就认为是同一个集合

  • 互异性：集合中任意两个元素都是不同的

二、操作

在ES6中，集合本身是一个构建函数Set，用来生成 Set 数据结构，如下：

const s = new Set();

关于集合常见的方法有：

  • add()：增

  • delete()：删

  • has()：改

  • clear()：查

add()

添加某个值，返回 Set 结构本身

当添加实例中已经存在的元素，set不会进行处理添加

s.add(1).add(2).add(2); // 2只被添加了一次

体现了集合的互异性特性

delete()

删除某个值，返回一个布尔值，表示删除是否成功

s.delete(1)

has()

返回一个布尔值，判断该值是否为Set的成员

s.has(2)

clear()

清除所有成员，没有返回值

s.clear()

关于多个集合常见的操作有：

  • 并集

  • 交集

  • 差集

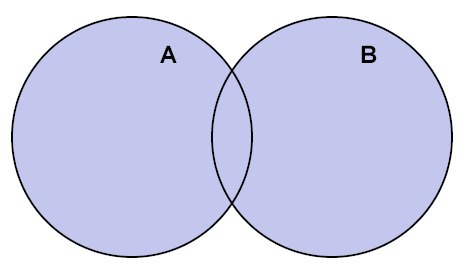
并集

两个集合的共同元素，如下图所示：

代码实现方式如下：

let a = new Set([1, 2, 3]);
let b = new Set([4, 3, 2]);

// 并集
let union = new Set([...a, ...b]);
// Set {1, 2, 3, 4}

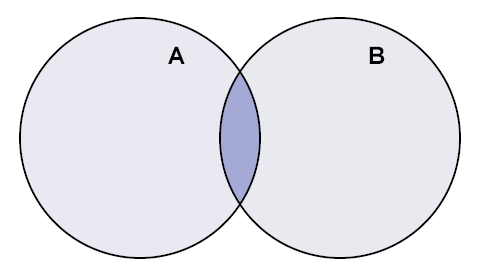
交集

两个集合A 和 B，即属于A又属于B的元素，如下图所示：

用代码标识则如下：

let a = new Set([1, 2, 3]);
let b = new Set([4, 3, 2]);

// 交集
let intersect = new Set([...a].filter(x => b.has(x)));
// set {2, 3}

差集

两个集合A 和 B，属于A的元素但不属于B的元素称为A相对于B的差集，如下图所示：

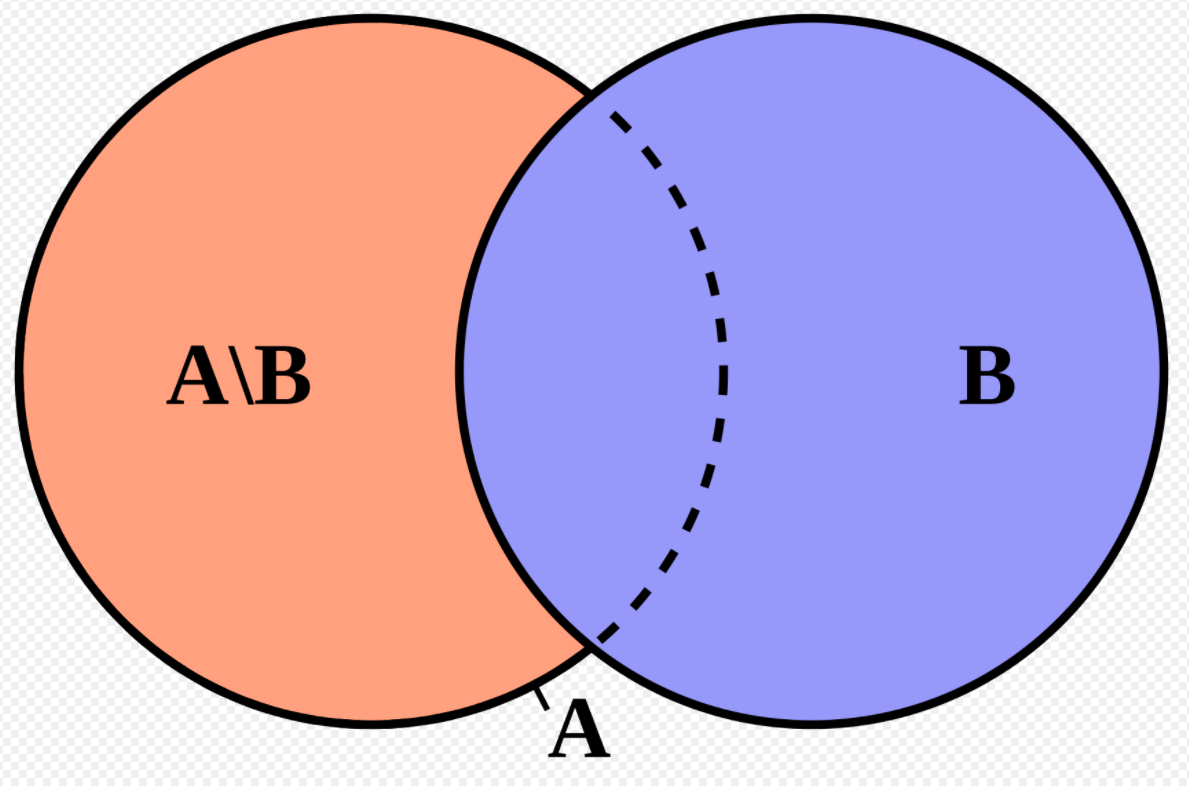
代码标识则如下：

let a = new Set([1, 2, 3]);
let b = new Set([4, 3, 2]);

// （a 相对于 b 的）差集
let difference = new Set([...a].filter(x => !b.has(x)));
// Set {1}

三、应用场景

一般情况下，使用数组的概率会比集合概率高很多

使用set集合的场景一般是借助其确定性，其本身只包含不同的元素

所以，可以利用Set的一些原生方法轻松的完成数组去重，查找数组公共元素及不同元素等操作

参考文献

ON THIS PAGE